My desire for more education has never sated, and I found a program at SDSU/UCI that was full of courses that were geared towards what I already did in my free time. Self taught in machine learning, app programming, database systems and a credentialed math teacher, it was like the computational science program was made specifically for me.
My name is Jared Brzenski. I am a PhD student working with Prof. Castillo at SDSU on mimetic ocean models. I also work with Prof. Kristen Davis numerically modeling flexible vegetation. I also work with assorted other faculty on projects from HPC to fluid-structure interactions.
Learning is my favorite activity. My dream job is to learn. My family has been very encouraging of me following my dream job. I enjoy continuing it through the UCI/SDSU joint doctoral program.
Research Advisor(s)
Jose E. Castillo and Kristen Davis
Research Abstracts
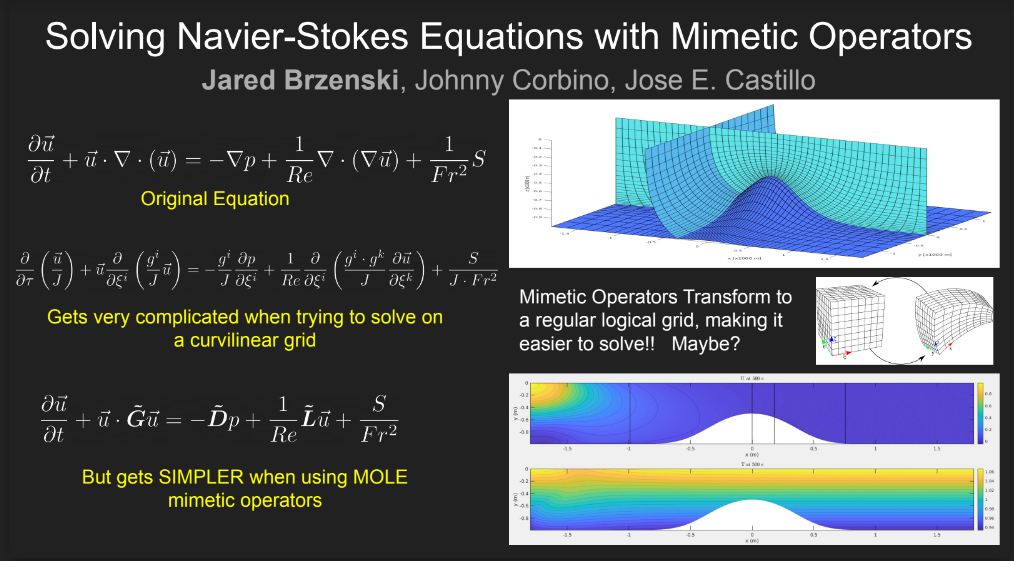
Mimetic Ocean Model:
Current ocean models rely on innovative schemes to deal with solving the Navier Stokes equations, and maintaining accuracy regardless of initial or boundary condition. Mimetic methods are discrete analogues of the gradient, divergence, and Laplacian operators Using mimetic methods, we seek to make a simple, fast RANS ocean model.
Flexible Vegetation:
Currently, vegetation in most ocean models is represented as rigid cylinders, which can account for some of the features of vegetation, but do not realistically capture the ability of vegetation to adapt to flow, or flex, thereby affecting the resultant calculations of turbulence, drag, and inertia in the water column. Existing flexible vegetation solvers use finite element schemes, which can be prohibitively expensive to calculate for large vegetative fields. I implement a finite difference scheme to solve the fourth order differential equation for highly flexible rods in a Lagrangian grid attached to the stems. This scheme is included in new subroutines created for SWASH, a shallow water ocean model, by calculating deflection on a moving subgrid, and returning the force exerted by the vegetative stem to the existing Navier-Stokes k-epsilon model at the appropriate computational grid points.
Click image to view research report presentation!